p-값의 올바른 해석: 통계적 유의성의 진정한 의미
통계적 추론의 세계에서 p-값(p-value)은 아마도 가장 자주 인용되면서도 가장 오해받는 개념일 것입니다. 논문, 연구 보고서, 뉴스 기사에서 "p < 0.05로 통계적으로 유의미하다"라는 문구를 자주 접하게 됩니다. 그러나 이 p-값이 정확히 무엇을 의미하며, 어떻게 해석해야 하는지에 대해서는 전문가들 사이에서도 혼란이 있습니다. 이번 포스트에서는 p-값의 정확한 의미와 올바른 해석 방법, 그리고 흔히 범하는 오류에 대해 알아보겠습니다.

p-값이란 무엇인가?
p-값(probability value)은 귀무가설이 참이라는 가정 하에, 관측된 결과나 그보다 더 극단적인 결과가 나올 확률을 의미합니다. 이는 가설검정의 핵심 요소로, 연구자가 설정한 유의수준(일반적으로 α = 0.05)과 비교하여 귀무가설의 기각 여부를 결정하는 데 사용됩니다.
즉, p-값은 "귀무가설이 참이라면, 우리가 관측한 것과 같거나 더 극단적인 결과를 얻을 확률"입니다.
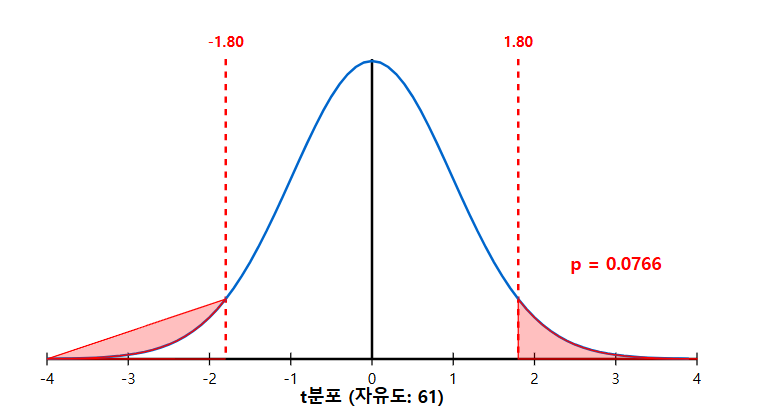
p-값의 올바른 해석
p-값을 올바르게 해석하기 위해서는 먼저 p-값이 무엇이 아닌지를 이해하는 것이 중요합니다:
- p-값은 귀무가설이 참일 확률이 아닙니다. p-값은 귀무가설이 참이라는 가정 하에 계산된 조건부 확률입니다.
- p-값은 연구 가설(대립가설)이 참일 확률이 아닙니다. p-값은 대립가설에 대한 직접적인 증거를 제공하지 않습니다.
- p-값은 효과의 크기나 중요성을 나타내지 않습니다. 통계적 유의성과 실질적 중요성은 별개의 문제입니다.
- p-값은 결과가 우연히 발생했을 확률이 아닙니다. p-값은 귀무가설 하에서의 데이터 발생 확률을 나타냅니다.
그렇다면 p-값은 어떻게 올바르게 해석해야 할까요?
p-값은 귀무가설에 대한 증거의 강도를 나타내는 지표로 볼 수 있습니다. p-값이 작을수록, 관측된 데이터가 귀무가설과 일치하지 않는다는 증거가 강해집니다. 그러나 p-값만으로는 어떤 가설이 참인지, 또는 연구 결과가 얼마나 중요한지를 결정할 수 없습니다.
p-값 해석의 실제 예시
다음 세 가지 시나리오를 통해 p-값의 올바른 해석을 살펴보겠습니다:
예시 1: 신약 효과 검증
한 제약회사가 새로운 고혈압 약물의 효과를 테스트하기 위해 임상 시험을 실시했습니다. 귀무가설은 "신약은 위약(placebo)과 효과가 동일하다"였고, 대립가설은 "신약은 위약보다 효과적이다"였습니다.
결과: p = 0.03
잘못된 해석: "신약이 효과적일 확률은 97%이다." 또는 "신약이 위약과 동일할 확률은 3%이다."
올바른 해석: "귀무가설이 참이라면(신약이 정말로 위약과 효과가 동일하다면), 우리가 관측한 것과 같거나 더 극단적인 효과 차이를 관찰할 확률은 3%이다. 이는 유의수준 5%보다 작으므로, 귀무가설을 기각하고 신약이 위약보다 효과적이라는 증거가 있다고 결론내릴 수 있다."
예시 2: 교육 방법 비교
두 가지 다른 교육 방법의 효과를 비교하는 연구에서, 귀무가설은 "두 방법 간 학습 효과의 차이가 없다"였습니다.
결과: p = 0.08
잘못된 해석: "두 교육 방법이 동일할 확률은 8%이다." 또는 "이 결과는 통계적으로 유의하지 않으므로, 두 방법은 확실히 동일하다."
올바른 해석: "귀무가설이 참이라면(두 교육 방법이 정말로 동일한 효과를 가진다면), 우리가 관측한 것과 같거나 더 극단적인 차이를 관찰할 확률은 8%이다. 이는 일반적인 유의수준 5%보다 크므로, 귀무가설을 기각할 충분한 증거가 없다. 그러나 이것이 두 방법이 동일하다는 증거는 아니며, 단지 차이가 있다는 것을 확신할 만큼의 증거가 부족하다는 의미이다."
p-값 해석의 흔한 오류
p-값을 해석할 때 흔히 범하는 오류들을 알아보겠습니다:
1. 이분법적 사고의 함정
p < 0.05이면 "효과가 있다", p ≥ 0.05이면 "효과가 없다"로 단순화하는 경향이 있습니다. 그러나 p = 0.049와 p = 0.051 사이에 본질적인 차이는 거의 없습니다. p-값은 연속적인 척도로 해석하는 것이 더 적절합니다.
2. 다중검정 문제 무시
여러 가설을 동시에 검정할 때, 각 검정마다 유의수준을 그대로 적용하면 1종 오류(가양성)의 확률이 증가합니다. 20개의 독립적인 가설을 α = 0.05로 검정하면, 적어도 하나의 거짓 양성 결과가 나올 확률은 약 64%입니다. 이런 경우, 본페로니 교정(Bonferroni correction)과 같은 방법으로 유의수준을 조정해야 합니다.
3. p-값 해킹(p-hacking)
원하는 결과를 얻을 때까지 데이터를 다양한 방식으로 분석하거나, 유의미한 결과만 선택적으로 보고하는 행위를 p-값 해킹이라고 합니다. 이는 과학적 연구의 신뢰성을 심각하게 훼손합니다.
4. 효과 크기 무시
p-값은 효과의 유무만 알려줄 뿐, 그 크기나 중요성에 대해서는 알려주지 않습니다. 통계적으로 유의미한 결과라도, 효과 크기가 작다면 실질적인 중요성은 낮을 수 있습니다. 따라서 p-값과 함께 효과 크기(effect size)도 함께 보고하고 해석하는 것이 중요합니다.
p-값 이상의 통계적 추론
p-값은 유용한 도구이지만, 이것만으로는 충분하지 않습니다. 통계적 추론을 더 풍부하게 하기 위한 다른 접근법도 알아봅시다:
1. 신뢰구간(Confidence Interval)
p-값은 귀무가설의 기각 여부만 알려주지만, 신뢰구간은 모수의 가능한 범위에 대한 정보를 제공합니다. 예를 들어, "평균 차이는 3.5이고 95% 신뢰구간은 [1.2, 5.8]이다"라는 결과는 효과의 크기와 정밀도에 대한 더 많은 정보를 제공합니다.
2. 베이지안 접근법(Bayesian Approach)
베이지안 통계는 사전 확률과 데이터를 결합하여 사후 확률을 계산함으로써, "귀무가설이 참일 확률"과 같은 직관적인 해석을 가능하게 합니다. 베이즈 인자(Bayes factor)는 두 가설의 상대적 증거 강도를 직접 비교할 수 있게 해줍니다.
3. 메타분석(Meta-analysis)
여러 연구 결과를 통합하여 분석하는 메타분석은 개별 연구의 한계를 극복하고 더 신뢰할 수 있는 결론을 도출하는 데 도움이 됩니다.
실전에서의 p-값: 어떻게 사용해야 할까?
연구자나 데이터 분석가로서 p-값을 더 효과적으로 사용하기 위한 몇 가지 제안을 드립니다:
- p-값과 함께 효과 크기를 항상 보고하세요. 통계적 유의성과 실질적 중요성을 함께 고려해야 합니다.
- 가능하면 신뢰구간을 함께 제시하세요. 이는 결과의 정밀도와 불확실성에 대한 더 많은 정보를 제공합니다.
- p-값을 연속적인 척도로 해석하세요. p = 0.04와 p = 0.06 사이에는 본질적인 차이가 거의 없습니다.
- 연구 설계와 가설을 사전에 명확히 하세요. 사후 가설(post-hoc hypotheses)은 p-값 해킹의 위험을 증가시킵니다.
- 결과를 맥락과 함께 해석하세요. 통계적 유의성은 결과의 과학적, 실용적 중요성을 보장하지 않습니다.
결론: 비판적 사고의 중요성
p-값은 통계적 추론의 유용한 도구이지만, 그 한계를 인식하고 비판적으로 해석하는 것이 중요합니다. 단순히 "p < 0.05이므로 효과가 있다"와 같은 기계적인 해석을 넘어, 연구의 맥락, 효과의 크기, 결과의 실질적 중요성을 종합적으로 고려해야 합니다.
데이터가 넘쳐나는 현대 사회에서, p-값을 올바르게 해석하는 능력은 과학적 문해력(scientific literacy)의 중요한 부분입니다. 이를 통해 우리는 더 나은 의사결정을 내리고, 과학적 지식의 발전에 기여할 수 있을 것입니다.
'Analysis' 카테고리의 다른 글
| 회귀분석의 기초: 단순 선형 회귀의 개념과 활용 (0) | 2025.03.06 |
|---|---|
| 통계적 추론에서의 1종 오류와 2종 오류: 의사결정의 두 얼굴 (2) | 2025.03.06 |
| 통계적 추론: 표본과 모집단, 가설검정의 원리 (0) | 2025.03.05 |
| 상관관계와 인과관계의 차이: 데이터 해석의 핵심 개념 (2) | 2025.03.04 |
| 기초 통계 개념: 확률 분포와 통계학의 두 가지 접근법 (0) | 2025.03.04 |



